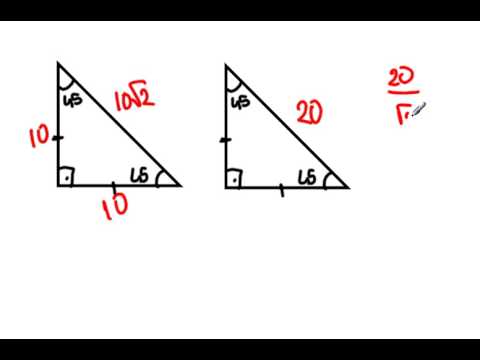
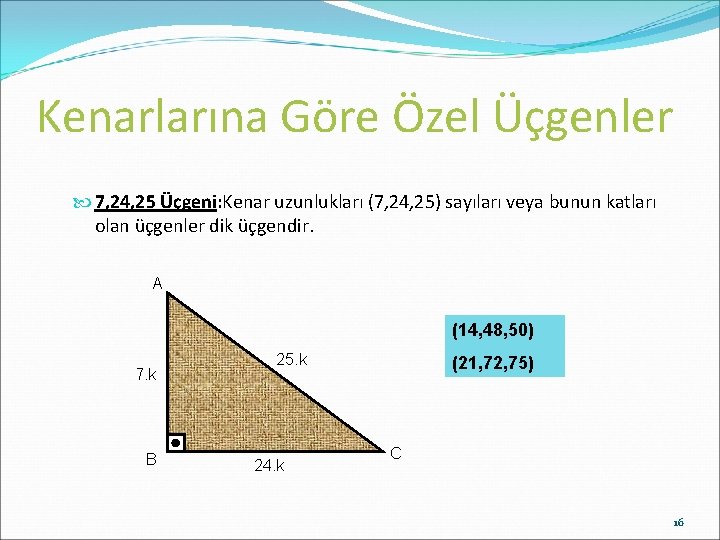
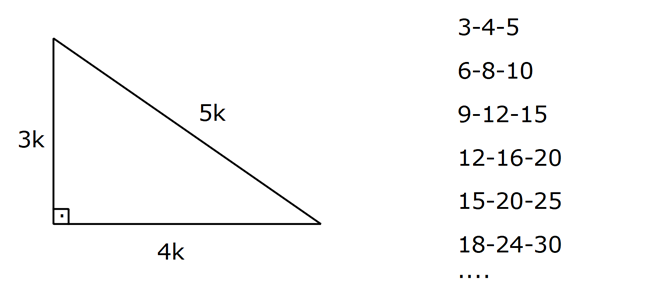
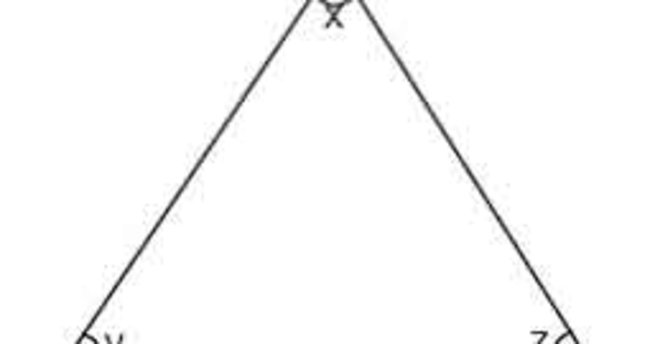
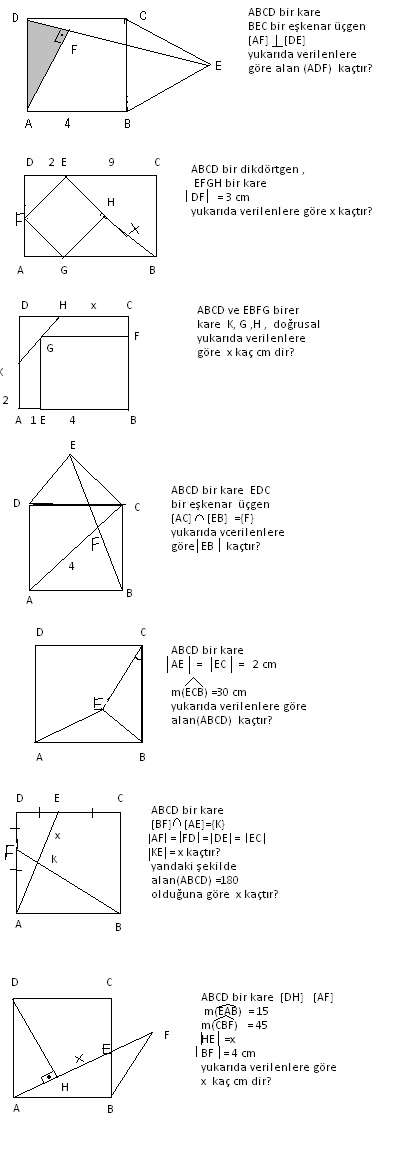
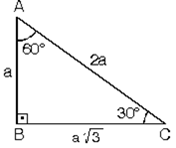
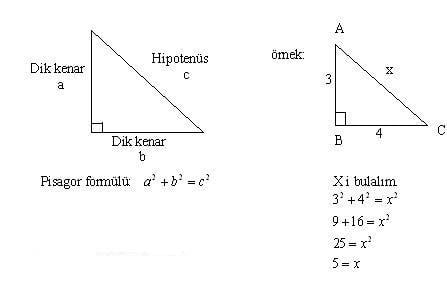
A) 6 B) 7 C) 8 D) 10 E) 12 wwwmatematikkolaynet Çözüm BCD üçgeni bir 30 60 90 üçgenidir 30 nin karşısı 12 ise 90 nin karşısı bunun iki katı yani 24 cm dir ABC üçgeni bir üçgenidir Bu üçgenin 1 yüksekliği, tabanın 'ü dür Bu sebeple;Proof Without Words kitabından şahane bir sözsüz kanıtDaha fazlası MY VİDEO EĞİTİM SİTESİ'nde Misafir olarak giriş yapabilirsiniz Detaylar için wwwmustafGeometri dersi, üçgenler konusu İkizkenar dik üçgenler, 30 60 90 üçgeni, 3 4 5 üçgeni, 5 12 13 üçgeni, 8 15 17 üçgeni Konu anlatımı ve örnekler
15 75 90 Ucgeni Kenar Bagintisi Ispat
90 75 15 üçgeni kenarları
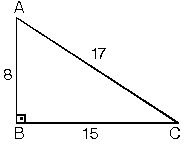
90 75 15 üçgeni kenarları- A) 9 B) 10 C) 12 D) 13 E) 14 ÇÖZÜM ADC üçgeni bir 3k – 4k – 5k üçgenidir O halde A açısı 90 dir ABC üçgeni de bir dik üçgen oldu Hipotenüsü 17 ve bir dik kenarı 8 cm O halde bu bir 8 1517 üçgenidir 15 75 90 üçgeni Genellikle geometri dersinde çok daha fazla karşılaştığımız bir özel üçgendir öğrenciler okul hayatları boyunca çeşitli yaşlarda ve sınıflarda bir çok sınava tabi tutulur Bu sınavlar sonucunda yetenek ve ilgi alanları, başarı olduğu dersler ve başarı boyutları belirlenir Ardından orta öğretim yaşına geldiğinde bu değerlendirmeler




lurplvgm7frm
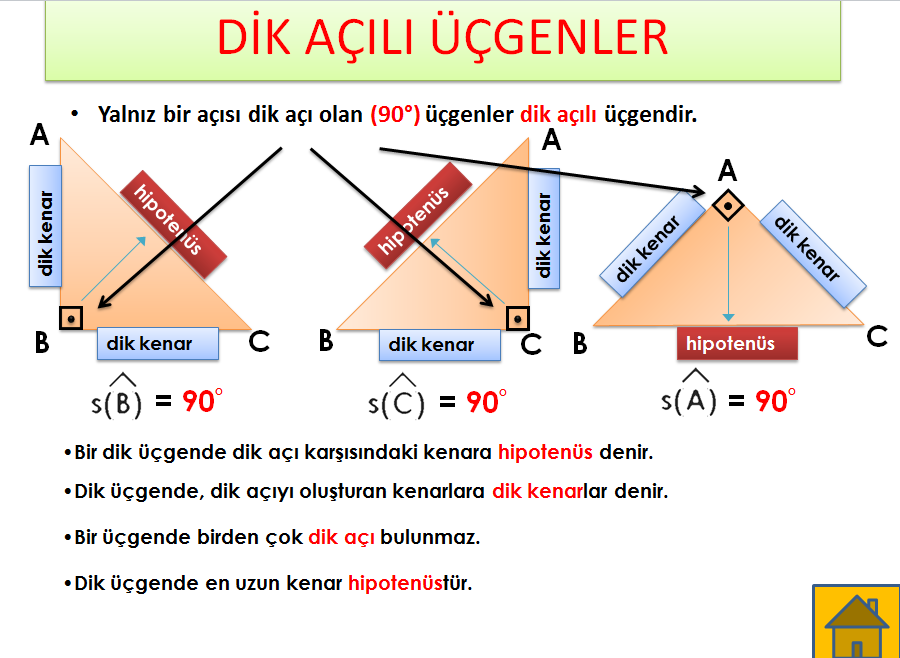
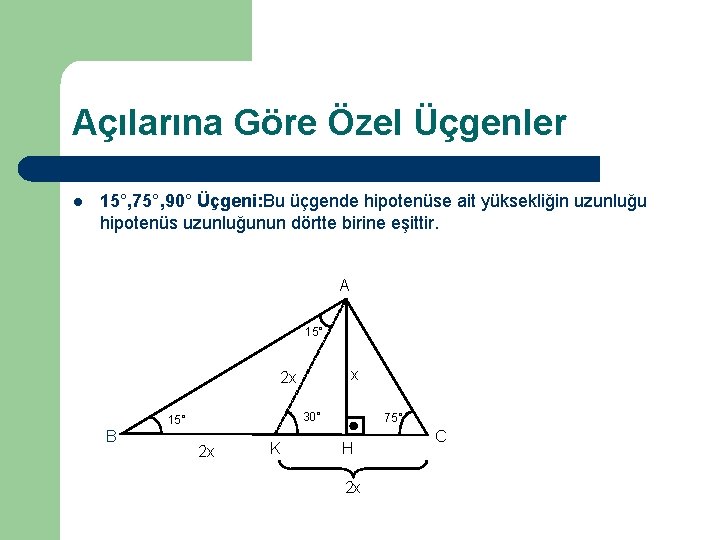
15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer açının ölçüsünü vermektedir İki dar açının birbirine oranı 1/5 olmalıdır Hipotenüse ait yükseklik hipotenüs uzunluğunun 4'te 1'idir4 24 x 6 cm bu 4 luruz 53Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardır
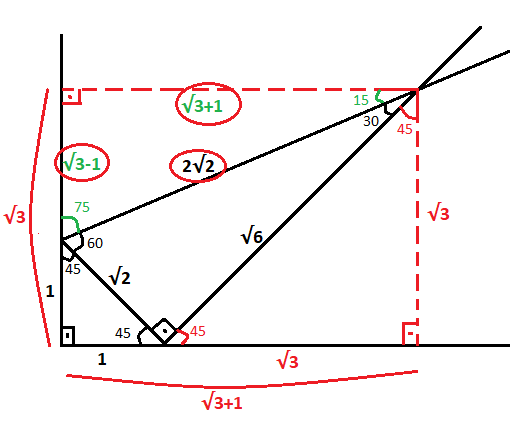
A) 3 B) 2 C) 2 2 D) 2 3 E) 4 Çözüm 135 'lik açının olduğu yerden, dışarıya doğru bir dik üçgen oluşturursak 45 – 45 – 90 üçgeni oluşur Bu üçgenin kenarları 6'şar cm olur Büyük üçgen de 6 8 10 üçgeni olduğundan; 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 inDİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 62 Kişisel Gelişim Geometri Psikoloji Science Harfler Eğitim Banyo Daha fazla bilgi Bunun gibi daha fazlası
(30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz ) İki kenarları aynı olduğu için iki açısı da aynı olur Ayrıca farklı uzunlukta olan kenara indirilen dikme hem açıortay hemde kenarortay olarak kabul edilir Açılarına göre üçgenler hangileridir?75 15 90 Üçgeni;




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik



15 75 90
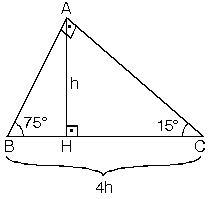
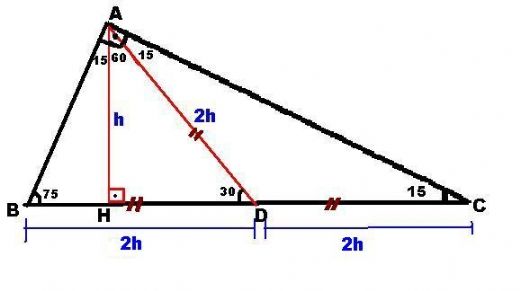
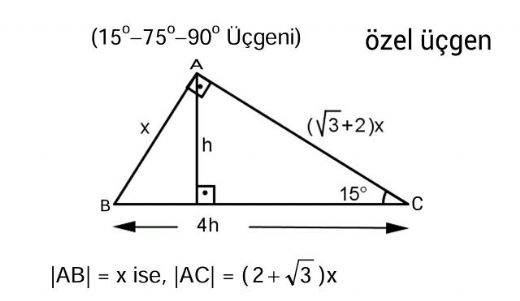
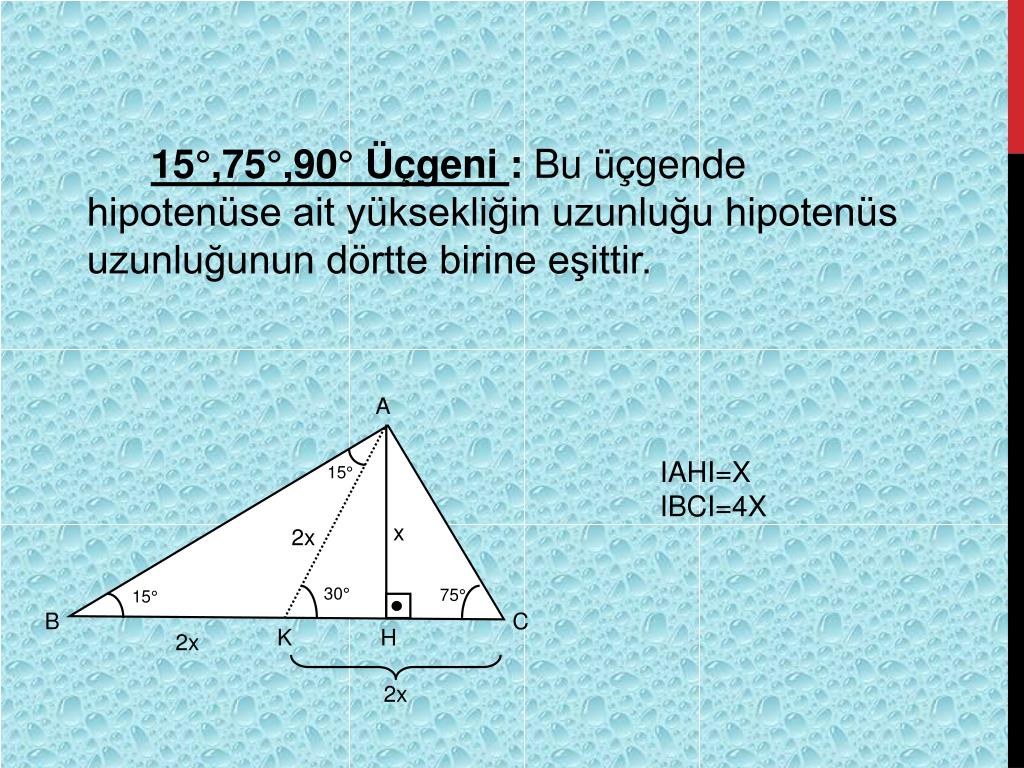
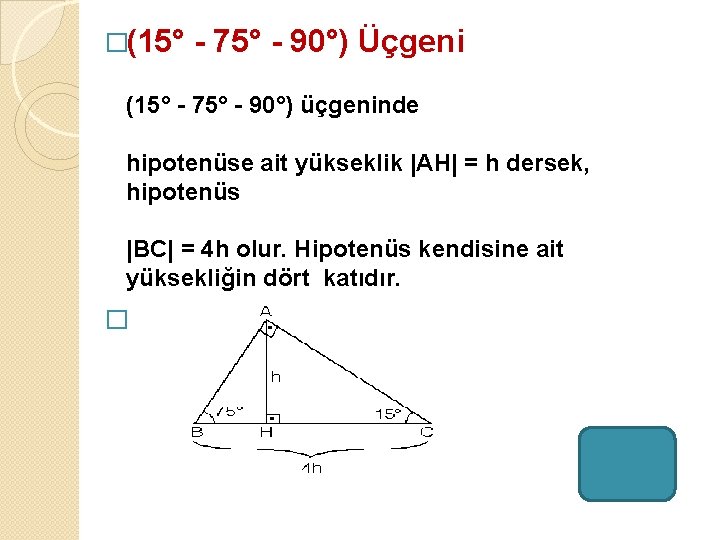
(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur15° – 75° – 90° Dik Üçgeni Yukarıda verilenlere göre, AC kaç cm dir?




Genler Gen Etler Ekenar Gen Kzkenar Gen Dk




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger
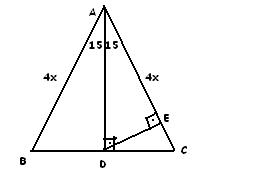
ペーパークラウン Paper Crown 紙で作る王冠 マゴクラ ダンボール ページェントの豪華な王冠ベクター フリー素材無料ダウンロード 高 作り方 画用紙で作る王冠 王さまのひげ付き Invidious 無料型紙 ベビーから大人まで使える 王冠の作り方 シロクマノート 紙 1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır İkizkenar Üçgen Özellikleri özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeni




Ozel Ucgenler




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi
(15 75 90) Üçgeni (45 45 90) Üçgeni;Dik açılı üçgen, 90 75 15 Üçgeni Üçgenin AlanıVeya üçgeni gördüğünüzde bu orana göre, biraz önce gördüğümüz oranlara göre kenar uzunluklarını bulabilirsiniz Mesela kenarları 2, 2 kök 3 ve 4 olan bir üçgen gördünüz 2'nin 2 kök 3'e oranı, 1 bölü kök 3 2'nin 4'e oranı da 1 bölü 2'dir Dolayısıyla bu üçgen üçgenidir




2 Kok 5 3 Ucgeni




15 75 90 Ucgeni Akilli Geometri
5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs15 75 90 Üçgeni Kenar Oranları 15 75 90 üçgeni kenarları belirli orana sahiptir Bu oranların ezbere bilinmemesi halinde kendiliğinden bulmak da mümkün olabilmektedir Fakat bu oranları bilmek soruların çözülmesi için daha büyük kolaylık sunacaktır Buna göre 15 75 90 üçgeninde 15 karşısı 1 birim kabul edilirse 75 15 75 90 Üçgeni Kuralları 15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış



Dik Ve Ozel Ucgenler Test 1



Dik Ucgende Trigonometrik Hesaplamalar
A) 12 B) 14 C) 15 D) 16 E) 18 Çözüm ABC üçgeni bir ikizkenar dik üçgendir Açıları 45 – 45 – 90 derece şeklindedir F ve E noktalarından birer dikme indirirerek, oluştur – duğumuz üçgenlerin kenarları 3'er ve 5'er cm olur15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönteDers içeriğini PDF olarak indirmek için http//wwwmetinhocamcom/dikucgen6Tüm PDF'leri tek dosya halinde indirmek için https//drivegooglecom/open?i




Mat Geo Fen Ucgenler Hakkinda Genel Hatirlatmalar 1 Orta Taban



ベスト 75 15 90 Ucgeni Ozellikleri シモネタ
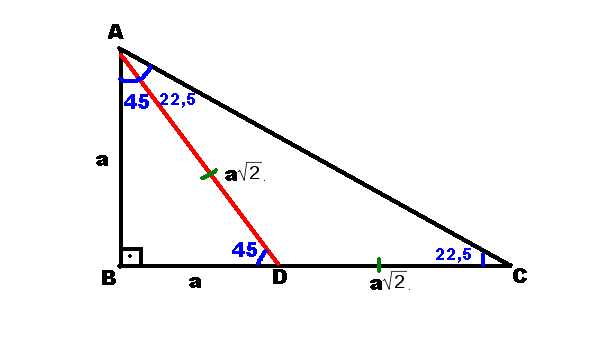
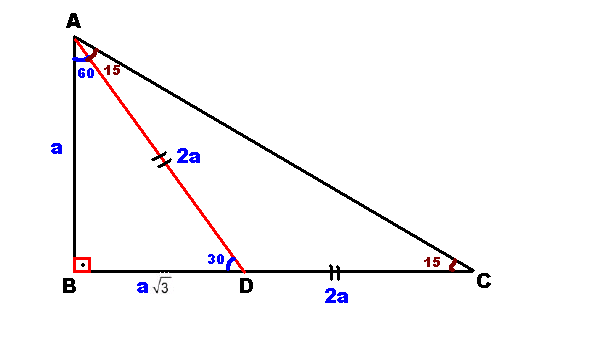
üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu 15 75 90 Üçgeni (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir Dik Üçgen ve Öklid KurallarıX 2 cm buluruz 11




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube



15 75 90 Ucgeni Ozellikleri
Alınan herhangi bir dik üçgenin kenarları arasındaki ilişkiye denir Bu ilişkiye gör Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur



Ozel Ucgenlerdeki Oranlari Ispatlayiniz 90 75 15 Matematik Kafasi



Dik Ve Ozel Ucgenler 1
90 75 15 üçgeni, Müfredat tarafından belirlenen kurallar ve işleyiş tablosuna göre genellikle daha çok sayısal ve eşit ağırlık öğrencilerinin öğrenmesi gereken konular arasındadır Bunun sebebi ise tamamen seçtikleri bölümden kaynaklıdır İlerideki girecek oldukları sınavlarda ancak kendi bölümlerindeki konulara hakim oldukları kadar başarı sergilerler Çünkü7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurüçgeninin kenarları arasındaki oranların ispatını öğrenin Orijinal video Sal Khan tarafından hazırlanmıştır Özel Dik Üçgenler Üçgeni Kenar Oranları İspatı Şu anda seçili olan öge bu Üçgeni Kenar Oranları Üçgeni ile İlgili Soru




30 60 90 Ucgeni Ve Ozellikleri Not Bu




上 75 15 90 Ucgeni Ozellikleri リタ ベルナル
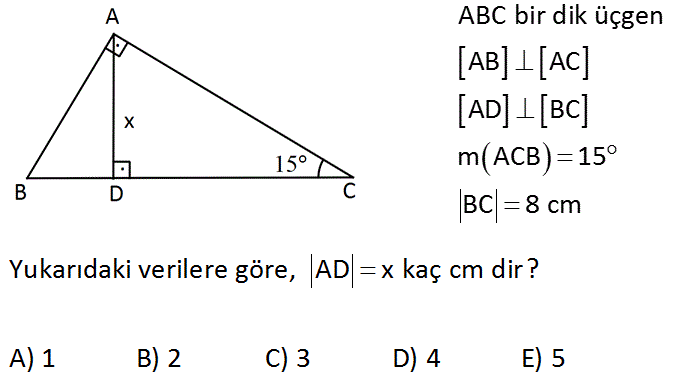
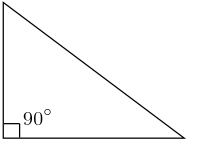
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m(A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardır (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdırABC üçgeninde AB ve AC kenarları dik kenarlardır BC kenarı hipotenüstür ve m(A) = 90° dir 15° 75° 90° üçgeni özel dik üçgen sınıfında yer alır m(A) = 90° olduğuna göre A köşesinden BC kenarına ait bir dikme ile yükseklik çizilir Bu yükseklik h ile gösterilirken BC kenarında H noktası ile işaretlenir




3 4 5 Ucgeni Ve Ozellikleri Not Bu




Ucgenlerde Uzunluk Matematik Ve Geometri
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik 15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgendKÜME EĞİTİMBUTİK DERSANE ANKARAİLKER ÇORSUZ



Monolib Encyclopedia Dictionary



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
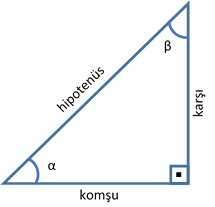
Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni1526 Hipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90 birim Karşı Kenar Uzunluğu 60,0001 birim Yukarıdaki ölçüleri bildiğimizi varsayalım Aşağıdaki α ve β açısının matematiksel hesaplama formülü nedir bununla alakalı bir bilgi paylaşılmamış α açısının ölçüsü 33,6901 derece β Hocam şöyle çözebilirsin a b c üçgenin kenarları A B C açıları olsunsinüs teoreminden herhangi bi kenar bölü karşısındaki açının sinüsü=diğer kenar bölü onun karşısındaki açının sinüsü bide şöyle bir bilgi daha vereyim 15 75 90 da 15in karşısı kök31, 75in karşısı kök31, 90 I'n karşısı 2kök2 ile orantılıdır yani sin15=kök31bölü 2kök2



22 5 67 5 90 Ucgeni 1 2 Ispat



最新 75 15 90 Ucgeni シモネタ
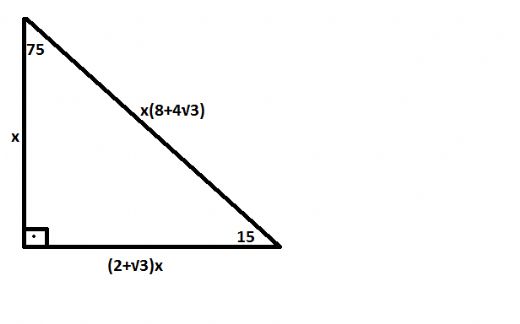
15 75 90 özel üçgeninin altın kuralı 15 derecenin karşısı 1 birim ise 75 derecenin karşısı √3 2 birim olmak zorundadır Hipotenüs ise 8 4√3 olarak hesaplanır Yukarıdaki kuralı uygulayabilmeniz için 15 75 90 özel üçgeninin var olması gerekiyor Bu üçgeni soru çözümlerinde sizler de elde edebilirsiniz Bu yazımızda 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı ve çok daha fazlası hakkında bilmen gerekenler ile Üçgende Açılar konusuna ait soruları çözerken işine yarayacağını düşündüğümüz ipuçları yer alıyor Umarız 15 75 90 Üçgeninde Dikme Özelliği 15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Yani dikme ile hipotenüs arasında h 4h bağıntısı vardır




15 75 90 Ucgeni Webders Net



15 75 90 Ucgeni Kenarlari Arasindaki Oran Eksi Up
15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğerÇözüm Pisagor bağıntısında 9 12 15 üçgeni diye bir özel üçgen olduğunu biliyoruz Öyleyse burada da B açısı 90 derece olsaydı x 15 olacaktı Ancak bu açı 90 dereceden büyük olduğu için x de 15'den büyük olacaktırA)8 B)6 C)5 D)4 E)3 30° – 30° – 1° Üçgeni 1° nin karşısındaki kenar, 30° nin karşısındaki kenarın katıdır Yukarıda verilenlere göre, x kaç cm dir?




Ucgende Metrik Bagintilar Cerezforum




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurIç açılarından bir tanesinin açı derecesi 90 olan üçgenlerdir Çemberde ise çapı tam göre açı ölçüsü 90 derece olurPisagor TeoremiPisagor teoremi;



Murat En Akdenz Nverstes Ge Nler 1




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




15 75 90 Ucgeni Kenar Bagintisi Ispat




15 75 90 Ucgeni Ve Dikdortgende Alan Youtube



1




Geometri 15 75 90 Ucgeni Nasil Olur Youtube




Dik Aci Ucgen Formulleri



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



45 45 90 Ucgeni Matematikce




Calameo Tyt Geometri 8 Ogrencilik Multi Kutu Test




Acilar Ve Ucgenler




15 75 90 Ucgeni Ozellikleri Ve Kurallari



15 75 90 Ucgeni




lurplvgm7frm




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular




Ozel Ucgenler Dik Ucgen Ppt Indir




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



15 75 90 Ucgeni




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



Ozel Ucgenler Konu Anlatimi



2




15 75 90 Ucgeni Not Bu



15 75 90 Ucgeni Turleri Ve Ozellikleri




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




15 75 90 Ucgeni Pow Bylge




Dortgen Vikipedi Cute766



15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr




30 60 90 Ucgeni Kenar Oranlari Ispati Geometri Trigonometri Youtube



1




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube



15 75 90 Ucgeni




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik



Acill Ozel Geometri Sorusu




Geometri Ucgende Acilar Eodev Cute766




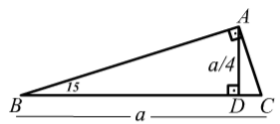
7 5 15 B Abc Ucgen Abe Eskenar Ucgen M Adc Geometri




Acilarina Gore Ucgenler Ppt Indir



Dik Ucgen Ozellikleri Nelerdir Egitim Haberleri




Zlltb9utgct6pm



1



Kare Sorulari Lutfen Yardimci Olurmusunuz Acillll




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri



Dik Ve Ozel Ucgenler 1



Ozel Dik Ucgenler Delinetciler Portal



90 75 15 Ucgeni 90 75 15 Ucgeni Ozellikleri Ucgen Gen Tr




Acilarina Gore Ozel Ucgenler Nelerdir



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



Geometri Formulleri Latest Version For Android Download Apk




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com



Zel Genler Dik Gen Zel Genler L L




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com




Dik Ve Ozel Ucgenler



Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id



15 75 90 Ucgeni 2 3 Ispat
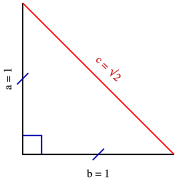



Dik Ucgen Vikipedi




Net Fikir Ekim




Ozel Ucgenler Nelerdir Ozel Acili Ve Dik Ikizkenar Ve Eskenar Ucgenler Formulleri Son Dakika Haberler



Zel Genler 1 Dk Gen 2 Kzkenar Gen



Googlegroups Com Attach 43d8bf14b3d04a My Ozelucgen Pdf Part 0 2 Vt Anajvre9l F1jaqjfwkexrzpbrgchtn5xw5psofg3jycbgcd Aypgkh Ze2mp1zt Hwd Zslphfbgabk Ycshseosnxsygw645gxjpg9wmoiwszlrfpbzo




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Calameo To Pdf Download Tool




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu



Dik Ucgen Vikipedi



Ozel Ucgenler




Ozel Ucgenler
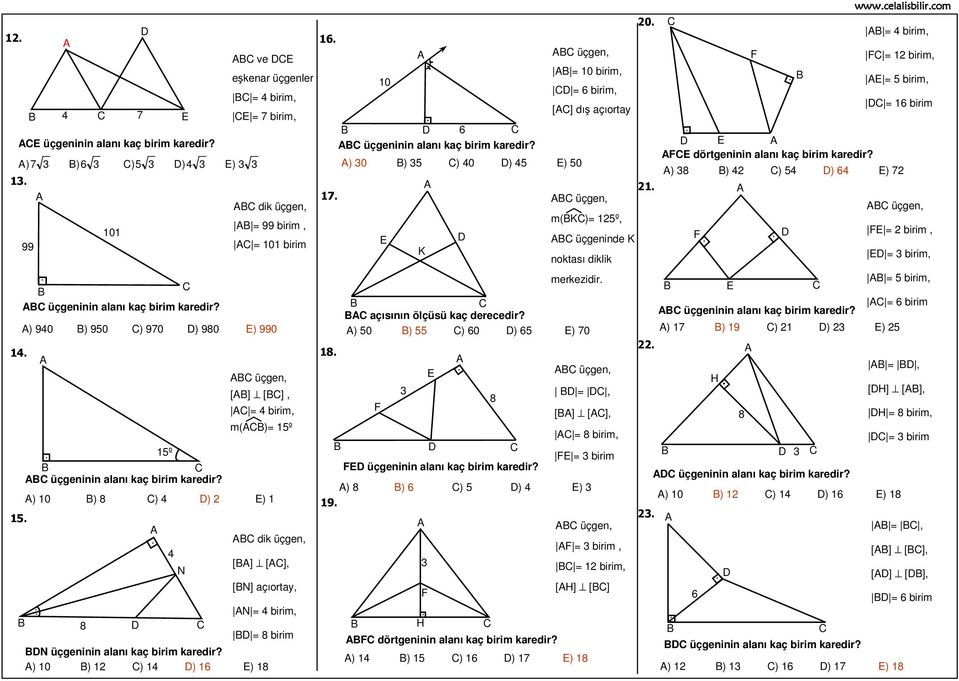



4 8 A D 2 Abc Ucgeninin Alani Kac Birim Karedir Abc Ucgeninin Alani Kac Birim Karedir A 16 B 18 C D 24 E º 135º Pdf Free Download
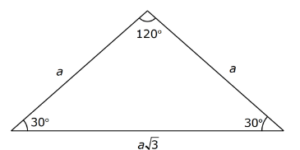



Ozel Ucgenler Konu Anlatimi




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com



Populer Icerik Ucgen Gen Tr



3




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




En Hizli 30 60 90 Ucgeni Kurali




Dik Ucgen Wikiwand
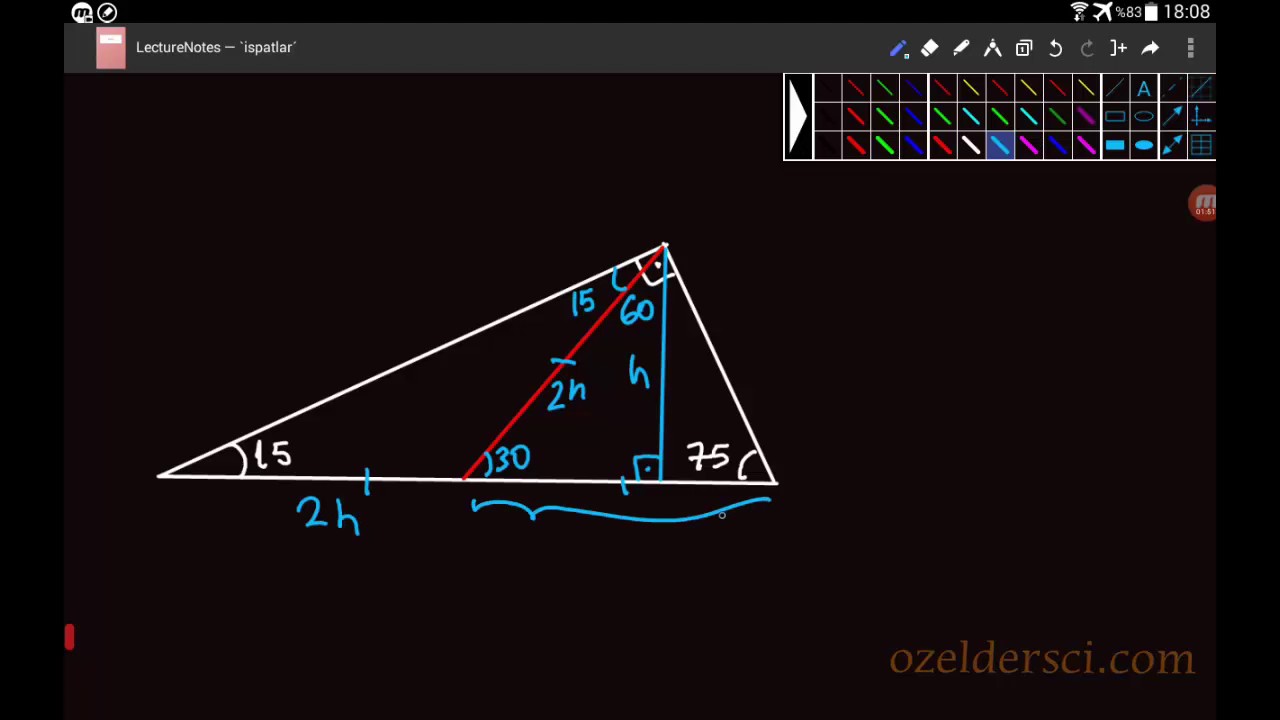



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube
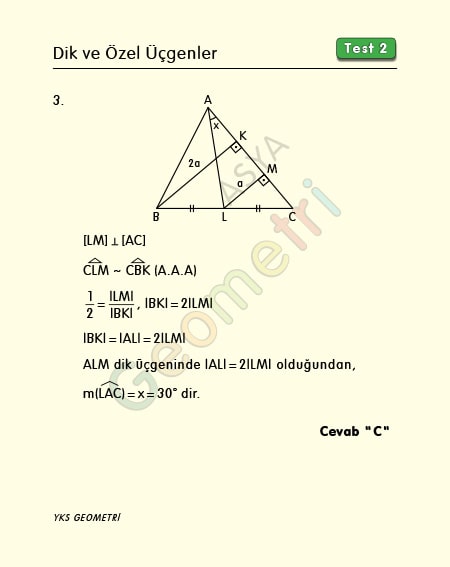



Dik Ve Ozel Ucgenler Test 2


